Lockhart's Lament
Pick an idea and stretch your brain!
I was sitting in a doctor’s waiting room, feeling bored and stuck, and I read Lockhart’s Lament.
I thought I read something like “There are fun and exciting puzzles everywhere around you!”1
🤔 Could that be true? How would I test that?
I checked my pockets and found these nifty dice I bought because I enjoy the pleasant hand feel of metal dice.
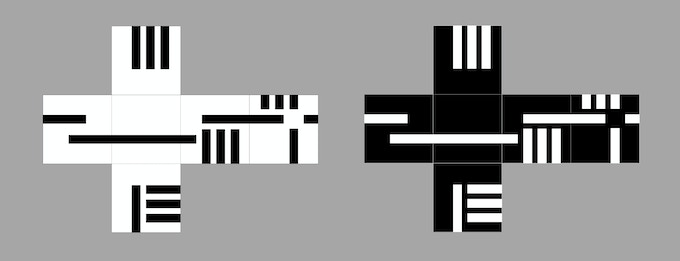
Where’s the puzzle?
I didn’t immediately see a puzzle. I stretched my brain a bit and wondered “Are these dice fair and balanced?”
I realized that the surface area of the etched grooves was different on different faces. That meant if the grooves were the same depth, these dice couldn’t possibly be fair because the sides wouldn’t weigh the same. After a bit more examination, the grooves appear to all be the same depth, and thus these dice could not possibly be balanced and fair.
Was that it? Were there more puzzles?
I noticed that each groove contributes to two different faces. Stretching my brain again, I wondered whether there were other valid arrangements of the grooves. Could one groove wrap entirely around the cube? If not, is there an arrangement with longer or shorter grooves?
Each groove contributes to the sum of the numbers on each side. Each groove crosses an edge between faces. All of the grooves are on exactly two faces, except one groove? Why? Could there be a different arrangement of grooves where each groove is only on two sides?
Graph Theory!
At some point, I realized this was a graph theory problem!
Days later I asked a mathematician friend of mine, and she told me several things.
She said, six sided dice are conventionally laid out so that opposite sides sum to 7. The opposite faces are 1 + 6, 3 + 4, and 2 + 5. If you add those up, the sum is 21. Because that’s an odd number, one of the grooves must cover an odd number of faces.
She said “Yes, this works for a tetrahedron.” and then drew the two possible four sided dice.
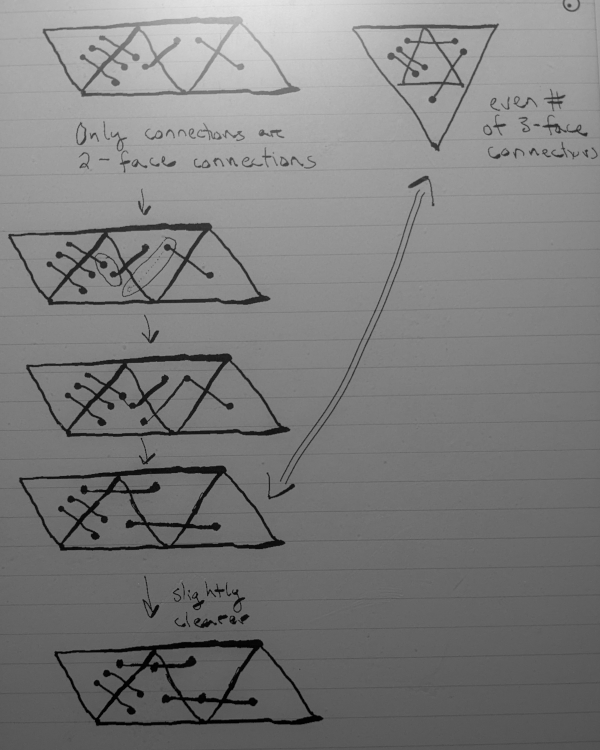
Does any arrangement of grooves work for eight sided dice? What about twenty sided dice?
I was then convinced that fun math puzzles really were everywhere! I just had to LOOK for them!
Notes
The creator of those dice I had in my pocket sells another set of dice with an entirely different layout.
Yes, those images are a picture of my remarkable 2, because I don’t know how to create diagrams. If you DO know, please tell me!
BONUS CONTENT
The same mathematician who got me started down this path (graph joke?) also drew alternate layouts for the cube:
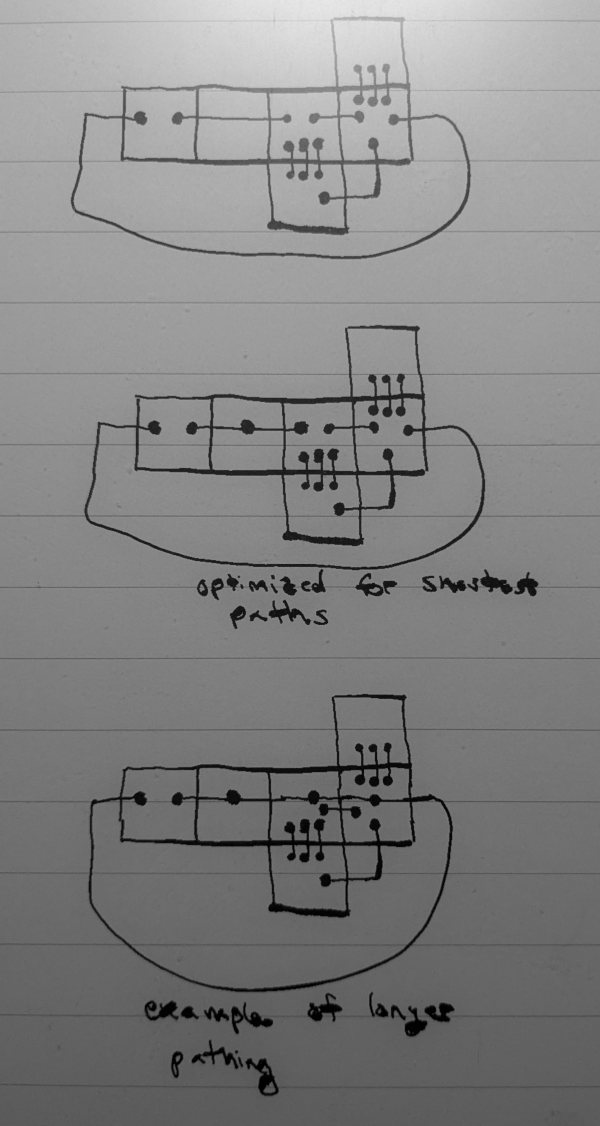
I know you did NOT come to this blog post to get a homework assignment, but maybe it’s not homework if I don’t know the answers?
Are there more layouts for the cube?
Does this work for all the Platonic solids? The Platonic solids are also called the Convex 3-polytopes, what about four dimensional solids?
If you know some of these answers, I want to know!
Even better, if you know of an English translation of Schläfli’s Theorie der vielfachen Kontinuität, I bet it has all these answers, and I WANT ONE VERY MUCH.
CONCLUSION
Lockhart is right, fun and exciting puzzles are everywhere, and math is a great way to explore them!
The actual text of what I read is:
↩︎A good problem is something you don’t know how to solve. That’s what makes it a good puzzle, and a good opportunity. A good problem does not just sit there in isolation, but serves as a springboard to other interesting questions.